|
#1
| |||
| |||
|
How can I get information about the B. sc. Mathematics program of the Jadavpur University??? Jadavpur University is a public state university located in Kolkata in the state of West Bengal in India. It was established in 1955. Please find the below attached file for the B.Sc. Hons. Mathematics JU-Syllabus: B.Sc. Hons. Mathematics JU-Syllabus  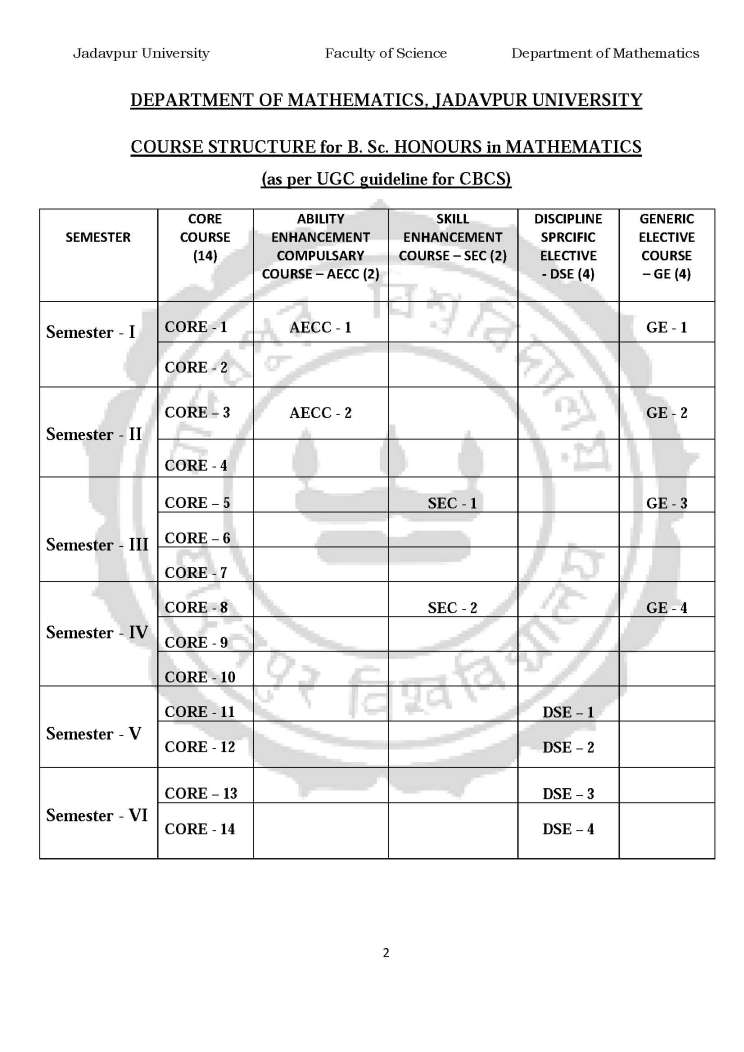 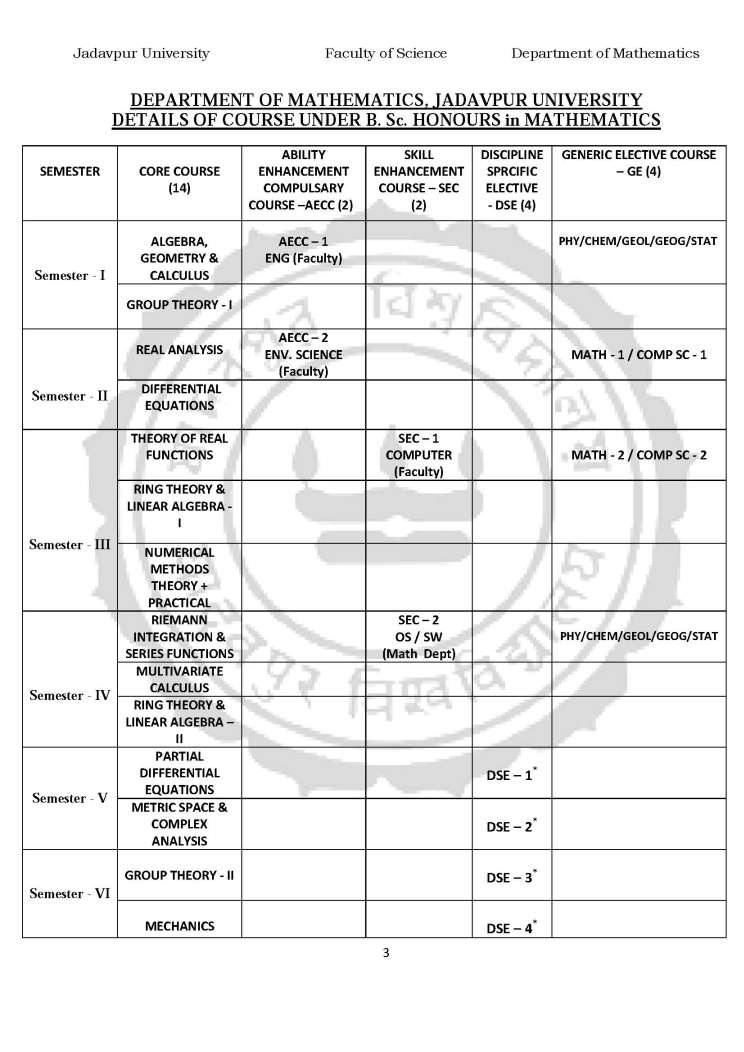 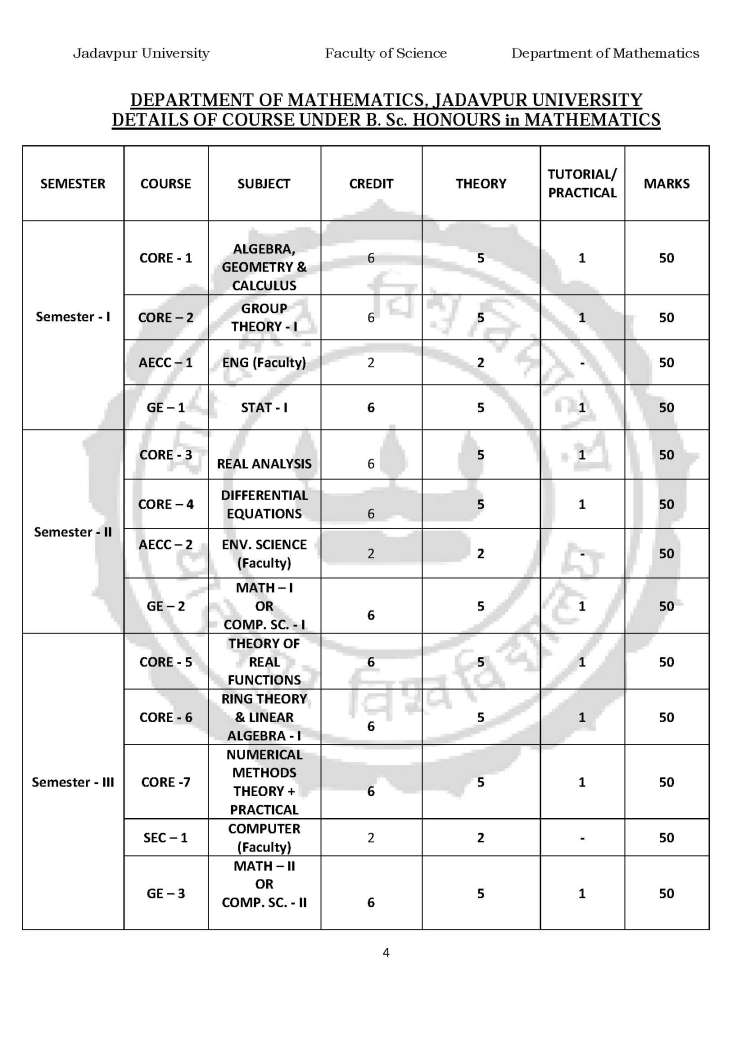 Eco Math Syllabus: UNIT – 1 General equation of second degree, concept of poles and polars, diameters & conjugate diameters, system of circles, Polar equation of a conic. Sphere, equation of circle in three dimensions, conicoids. Jadavpur University Faculty of Science Department of Mathematics 40 UNIT – 2 Triple products of vectors – its properties and application to geometry and mechanics. Vector functions: gradient, divergence, curl, line, surface, volume integral and allied theorems. UNIT – 3 Successive differentiation and Leibnitz theorem. Rolle’s theorem (statement only), Lagrange’s mean value theorem, Taylor’s theorem, Maclaurin’s series and expansion of standard function, Indeterminate forms, Maxima and Minima, point of inflexion. Function of several variables – limit, continuity, partial derivatives. Euler’s theorem. Fundamental theorem of integral calculus, properties of definite integrals, Improper integrals, Beta and Gamma functions, application of definite integrals to geometric problems. Multiple integrals. Address: Main Campus 188, Raja S.C. Mallick Rd, Kolkata - 700032. Salt Lake Campus Plot No.8, Salt Lake Bypass, LB Block, Sector III, Salt Lake City, Kolkata - 700106. Last edited by Aakashd; February 27th, 2020 at 12:59 PM. |
|
#2
| |||
| |||
|
Here are the details of the B. sc. Mathematics program of the Jadavpur University: Eligibility The candidate should have completed 10+2 with mathematics subject and good academic record from any recognized board of India… Duration 3 years Syllabus Here is the syllabus of the program: Matrix Theory and Linear Algebra in R". Systems of linear equations, Gauss elim-ination, and consistency. Subspaces of R", linear dependence, and dimension. Ma-trices, elementary row operations, row-equivalence, and row space. Systems of linear equations as matrix equations, and the invariance of its solution set under row-equivalence. Row-reduced matrices, row-reduced echelon matrices, row-rank, and using these as tests for linear dependence. The dimension of the solution space of a system of independent homogeneous linear equations. Linear transformations and matrix representation. Matrix addition and multipli-cation. Diagonal, permutation, triangular, and symmetric matrices. Rectangular matrices and column vectors. Non-singular transformations. Inverse of a Matrix. Rank-nullity theorem. Equivalence of row and column ranks. Elementary matrices and elementary operations. Equivalence and canonical form. Determinants. Eigen-values, eigenvectors, and the characteristic equation of a matrix. Cayley-Hamilton theorem and its use in finding the inverse of a matrix. Remaining syllabus is in the attachment click on it…
__________________ Answered By StudyChaCha Member |