EEE 5th Sem Syllabus GGSIPU

Hello sir, my brother is looking for syllabus for EEE 5th sem from Guru Gobind Singh Indraprastha University please provide me?

The Guru Gobind Singh Indraprastha University is provides its syllabus for all candidates in PDF form.

As you want here I’m giving you Syllabus for EEE 5th sem from Guru Gobind Singh Indraprastha University:


Syllabus for EEE 5th sem from Guru Gobind Singh Indraprastha University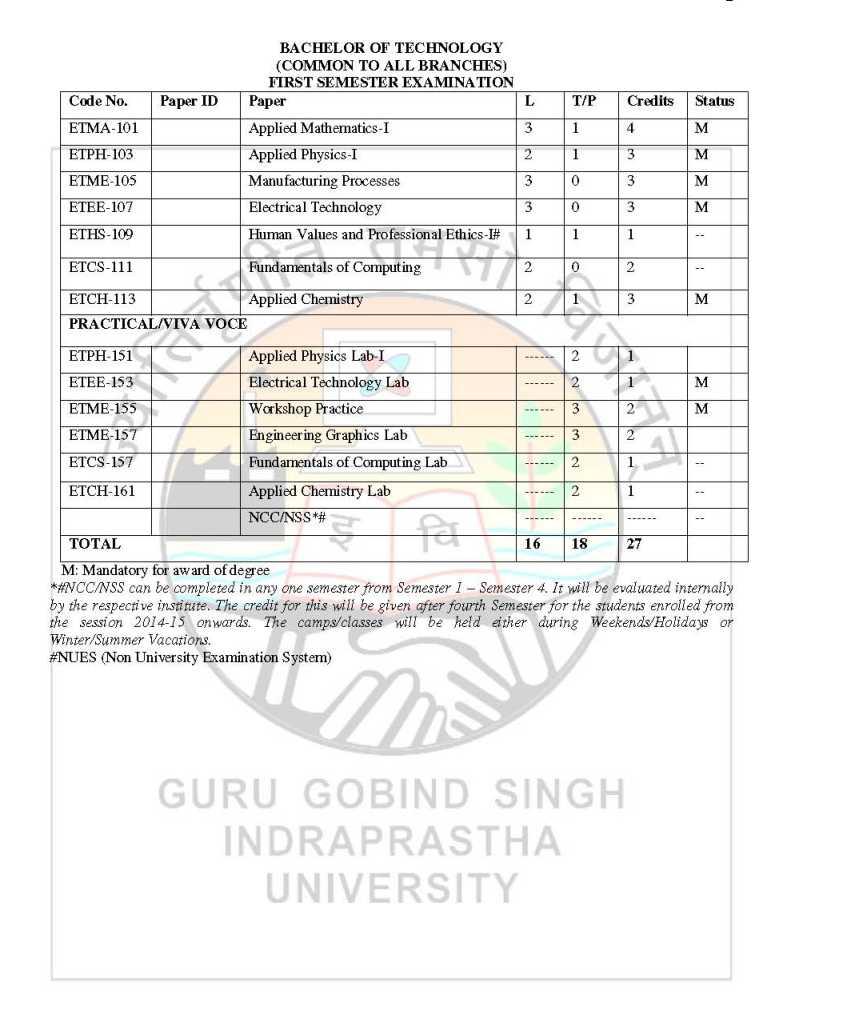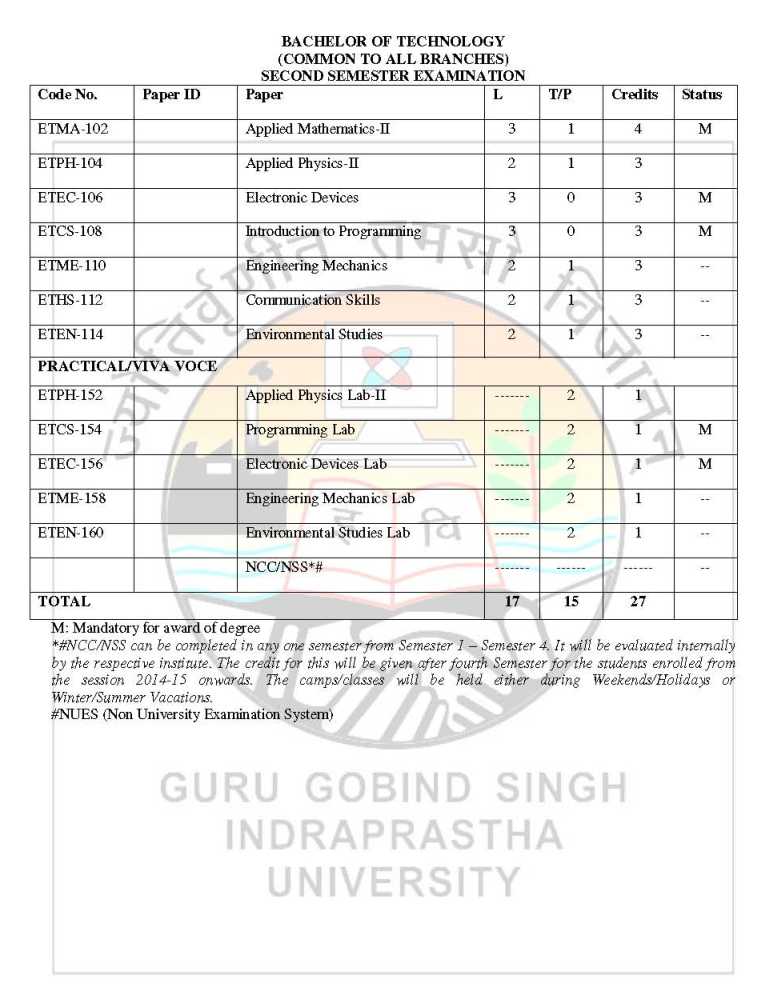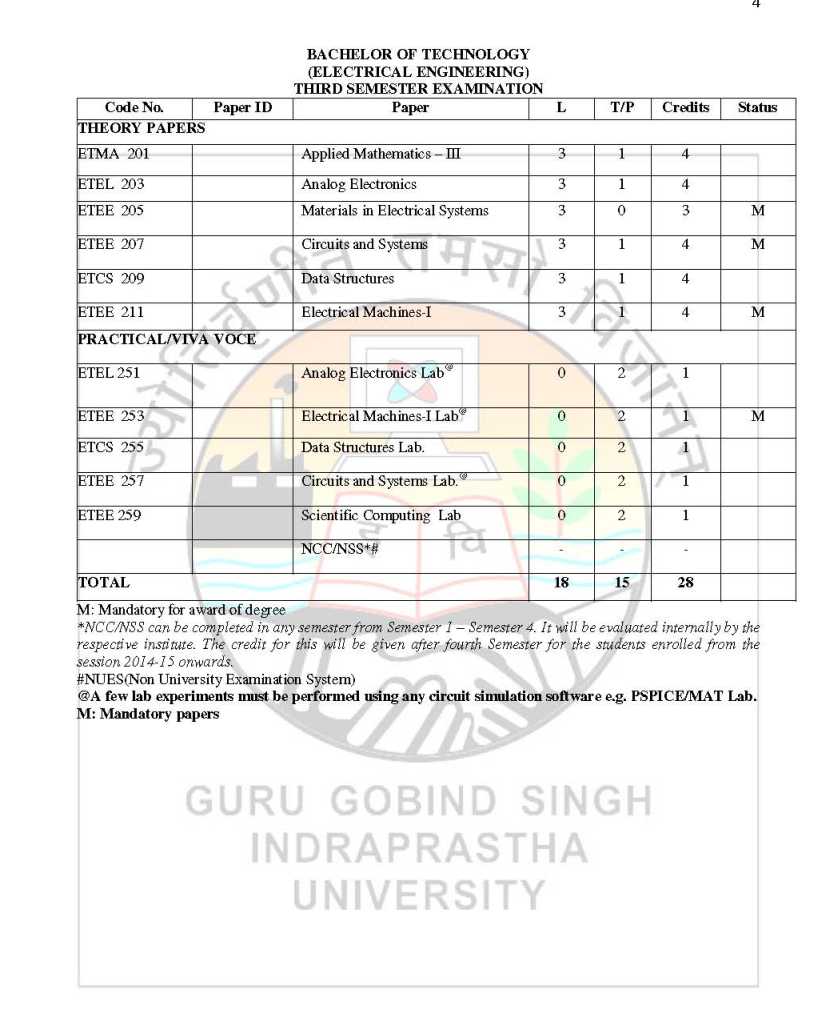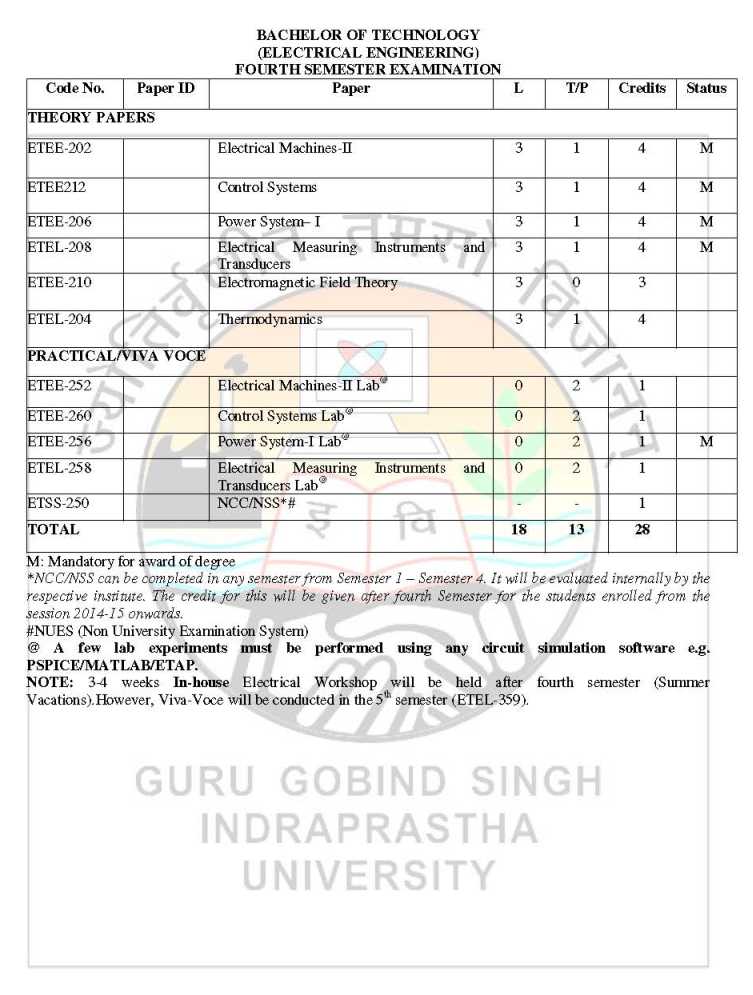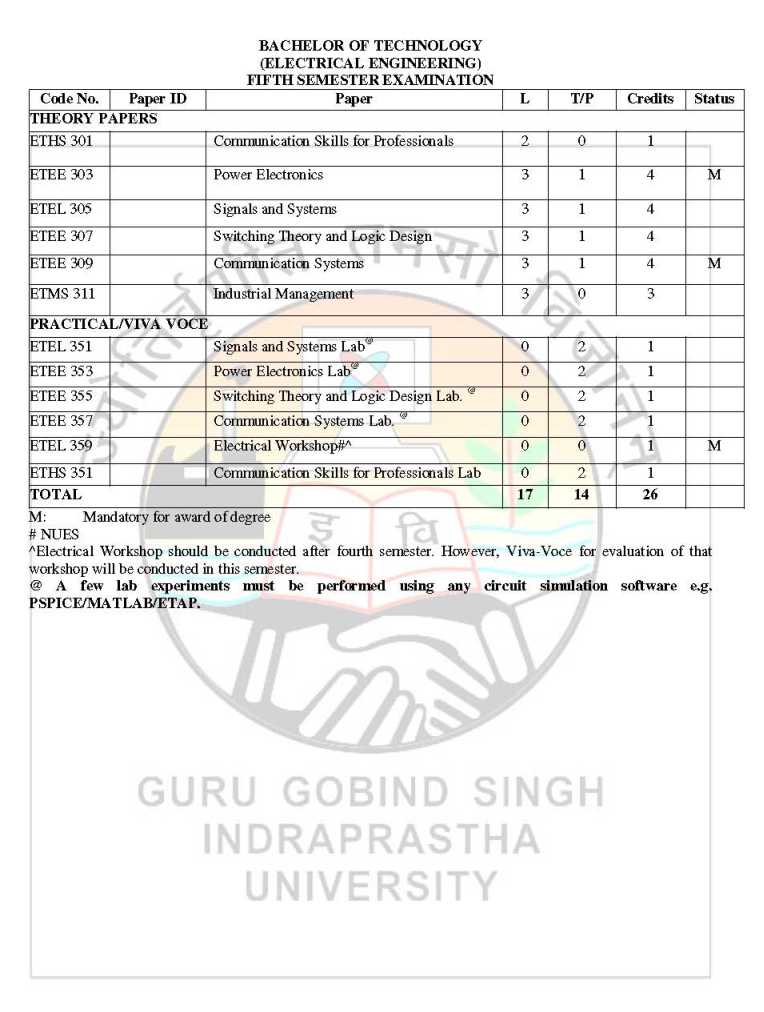







Here I’m attaching PDF of syllabus for EEE 5th sem from Guru Gobind Singh Indraprastha University:

Syllabus for EEE 5th sem:

Paper Code: ETMA-101
Paper: Applied Mathematics – I

Question No. 1 should be compulsory and cover the entire syllabus. This question should have objective or short answer type questions. It should be of 25 marks.
Apart from question no. 1, rest of the paper shall consist of four units as per the syllabus. Every unit should have two questions. However, student may be asked to attempt only 1 question from each unit. Each question should be of 12.5 marks.

UNIT I
COMPLEX NUMBERS AND INFINITE SERIES: De Moivre’s theorem and roots of complex numbers. Euler’s theorem, Logarithmic Functions, Circular, Hyperbolic Functions and their Inverses. Convergence and Divergence of Infinite series, Comparison test d’Alembert’s ratio test. Higher ratio test, Cauchy’s root test. Alternating series, Lebnitz test, Absolute and conditioinal convergence.

UNIT II
CALCULUS OF ONE VARIABLE: Successive differentiation. Leibnitz theorem (without proof) McLaurin’s and Taylor’s expansion of functions, errors and approximation.
Asymptotes of Cartesian curves. Curveture of curves in Cartesian, parametric and polar coordinates, Tracing of curves in Cartesian, parametric and polar coordinates (like conics, astroid, hypocycloid, Folium of Descartes, Cycloid, Circle, Cardiode, Lemniscate of Bernoulli, equiangular spiral). Reduction Formulae for evaluating

Finding area under the curves, Length of the curves, volume and surface of solids of revolution.

UNIT III
LINEAR ALGEBRA – MATERICES: Rank of matrix, Linear transformations, Hermitian and skeew – Hermitian forms, Inverse of matrix by elementary operations. Consistency of linear simultaneous equations, Diagonalisation of a matrix, Eigen values and eigen vectors. Caley – Hamilton theorem (without proof).

UNIT IV
ORDINARY DIFFERENTIAL EQUATIONS: First order differential equations – exact and reducible to exact form. Linear differential equations of higher order with constant coefficients. Solution of simultaneous differential equations. Variation of parameters, Solution of homogeneous differential equations – Canchy and Legendre forms.

Attached Files Available for Download

Syllabus for EEE 5th sem from Guru Gobind Singh Indraprastha University.pdf (833.2 KB, 9 views)

__________________
Answered By StudyChaCha Member